Вклад Л.В. Канторовича в экономическую науку

Автор: Кирик Владимир Михайлович,

Норильский Государственный Индустриальный Институт

Научный руководитель: Белоусова Елена Вячеславовна, доцент

г.Норильск, 2020

Аннотация: В исследовании автором обобщен вклад Л.В. Канторовича в экономическую науку". Целью работы является исследование вклада Л.В. Канторовича в экономическую науку. Вклад, сделанный замечательным и талантливым ученым Леонидом Витальевичем Канторовичем в различные области математики и экономики, имел огромное значение в развитии решения прикладных производственных задач.

Задачи исследования: обозначить роль Канторовича в области математической экономики, описать базовые методы оптимального использования ресурсов, рассмотреть метод ньютона-Канторовича приближенного нахождения решений квадратных матричных уравнений. Автор приходит к выводу, что каждая из предметных областей вносит свои дополнительные требования в способ решения задач, и, следовательно, в способ адаптации известных алгоритмов. В настоящее время существующие методы решения нелинейных матричных уравнений очень громоздки и могут быть применены к ограниченным классам уравнений. Поэтому, в настоящей работе была поставлена цель - разработать эффективный приближенный метод решения квадратных матричных уравнений
В работе сделана попытка разработки эффективного приближенного метода нахождения решения квадратных матричных уравнений, основанный на использовании модифицированного метода Ньютона-Канторовича

Актуальность. На развитие экономической мысли повлиял такой гениальный советский математик и экономист, как Канторович Леонид Витальевич - один из создателей линейного программирования. Вклад, сделанный замечательным и талантливым ученым Леонидом Витальевичем Канторовичем в различные области математики и экономики, имел огромное значение в развитии решения прикладных производственных задач.

Биографические данные. Лауреат Нобелевской премии по экономике 1975 года "за вклад в теорию оптимального распределения ресурсов". Л.В. Канторович вошел в плеяду крупнейших ученых XX в. благодаря своему капитальному вкладу в математику и экономику. Его исследования в области дескриптивной теории функций и множеств, функционального анализа, вычислительной математики, теории экстремальных задач, вычислительной техники (от теории программирования на ЭВМ до конструирования самих машин) отличались, с одной стороны, новизной идей, а с другой - естественностью подходов и потому послужили основой для формирования многих новых научных направлений.

Кроме того, его концепция оптимальной экономической модели на макроэкономическом уровне и сегодня обладает огромным потенциалом. И в речи шведского профессора Рагнара Бентзеля, которую в 1975 г. он произнес, представляя лауреатов Нобелевской премии по экономике Л. В. Канторовича и Т. Купманса, отмечено всеобщее значение концепции для любой экономики, независимо от ее социальнополитической формы: "Поскольку запас производственных ресурсов всюду ограничен, каждое общество сталкивается с кругом вопросов, касающихся оптимального использования имеющихся ресурсов и справедливого распределения доходов между гражданами. Точка зрения, с которой могут рассматриваться подобные нормативные вопросы, не зависит от политической организации рассматриваемого общества". Поэтому исследование и разработка методов Работа поддержана грантом РФФИ 12-07-00631-а. решения задач рационального использования ресурсов актуальны и по сей день.

1.Исследования Канторовича в области математической экономики

Обращаясь непосредственно к теме исследований Канторовича в области математической экономики, необходимо вначале назвать основные исследования по этой тематике, проведенные Леонидом Витальевичем в довоенные годы. Без всякого сомнения, особое место в его научной биографии занимает работа "Математические методы организации и планирования производства"[1], поскольку это первая публикация на тему ЛП, как в творчестве Леонида Витальевича, так и в мире в целом. В ней поставлены основные задачи ЛП, дан метод их решения и рассмотрены важнейшие области применения (как позднее напишет Дж. Б. Данциг, "работа Л. В. Канторовича 1939 г. содержит почти все области приложений, известные в 1960 г."[2]). Значение работы 1939 г.[3] для математики состоит в изложенном и обоснованном в ней методе решения задачи на экстремум, выходящем за рамки классического математического анализа. Здесь приведен алгоритмический метод решения проблемы и два подхода к доказательству существования решения.

Родилась эта работа, как и глубокое увлечение ученого разработкой математических методов в экономике, в известной степени случайно. В 1938 г. Канторович занялся линейной оптимизацией, решая частную задачу оптимальной загрузки станков, с которой в Институт математики и механики ЛГУ обратился фанерный трест. Задача была абсолютно практическая и частная, однако Леонид Витальевич в силу свойственной ему способности видеть, не останавливаясь на частных моментах, целостный результат, общую картину, заметил, что многие другие экономические проблемы приводят к аналогичным математическим задачам - максимизации функции при многих ограничениях.

Отметим, что часто при решении практических задач не получается напрямую применить методы математического анализа, так как это приводит к десяткам тысяч, а иногда и миллионов, систем уравнений, что делает такой подход неприменимым на практике. Канторович предложил геометрический метод, доклад о котором, по воспоминаниям автора, впервые был сделан на октябрьской научной сессии Ленинградского педагогического института им. А. И. Герцена в 1938 г. Метод этот, однако, был недостаточно алгоритмичен, в связи с чем исследования продолжились, и уже в конце 1938 г. Канторович в связи с некоторыми идеями функционального анализа сформулировал общий метод решения подобных задач - метод разрешающих множителей. Данный метод, который показался ему перспективным как в силу его алгоритмичности, так и благодаря содержательному экономическому значению самих множителей, в течение нескольких месяцев выявленному автором, оказался одним из простейших и эффективнейших численных методов ЛП, и мог быть использован для решения практических задач уже в то время

Также в данной работе был выяснен экономический смысл разрешающих множителей, рассмотрены вопросы их использования при вариации плана, определения показателей эффективности продукции и кооперирования предприятий.

Вскоре после книги 1939 г., в которой содержалась постановка задачи выбора самого выгодного из огромного числа вариантов посредствам минимизации линейной функции на множестве, задаваемом линейными ограничениями типа равенств и неравенств, и была изложена разработанная Канторовичем теория этих задач вместе с предложенными ученым методами их решения, Леонид Витальевич продолжил исследования математических методов, применимых в экономике.

Его дальнейшие исследования по этой теме можно разделить на две группы: те, которые были ориентированы на практическое применение и носили более частный характер, и те, которые имели большее теоретическое значение, не соотносясь с конкретными экономическими примерами.

2.Базовые методы оптимального использования ресурсов

Основополагающую роль в становлении и развитии теории оптимального использования ресурсов и линейного программирования сыграла опубликованная профессором Л. В. Канторовичем в 1939 г. брошюра[4], где рассматривались различные практические задачи организации производства, в которых требовалось найти наилучший вариант решения. Книга была написана после консультации сотрудников Фанерного треста по вопросам решения задач, которые не удавалось решить традиционными в то время методами. Л. В. Канторович предложил метод разрешающих множителей (индексов), который устанавливает принципиальную возможность нахождения наилучшего решения для многих задач народного хозяйства, в том числе и для задачи массового раскроя. Несмотря на огромный круг научных интересов, в последующие годы Л. В. Канторович неоднократно возвращался к проблеме рационального раскроя, например[5].

В 30-х гг. прошлого века были заложены основы теории раскроя пиловочного сырья, основоположником которой стал Х. Л. Фельдман[6]. Он предложил математический подход для решения задачи о максимальных поставах при распиловке бревен. Вместе со своими последователями он создал систему, ориентированную на максимизацию объемного и качественного выхода обрезных пиломатериалов. Точная математическая схема решения не в полной мере учитывала реальные условия, такие как качественные характеристики сырья и пилопродукции, поэтому результаты на практике могли быть и неверными. Позднее В. А. Залгаллером разработан графический метод составления максимальных поставов, основанный на геометрическом признаке экстремума. Предложенный

В. А. Залгаллером метод позволил приблизить теорию максимальных поставов к условиям производства[7].

Разработанная и усовершенствованная теория, однако, и в настоящее время не может дать ответа на многие проблемы технологии лесопиления, в связи с чем актуально ее дальнейшее совершенствование. Среди основных причин этого явления: технический прогресс, изменения размерно-качественной характеристики поступающего в раскрой пиловочного сырья и его породного состава, ужесточение требований экологов, изменение действующих стандартов на сырье и пиленую продукцию.

Задачи раскроя представляют собой важную технологическую проблему, оптимальное решение которых позволяет минимизировать расход имеющихся ресурсов. Это такие задачи, как:

• раскрой линейного материала;
• продольная резка лент и рулонов;
• раскрой листов на прямоугольные заготовки;
• использование материалов смешанной длины;
• раскрой для серийных и несерийных изделий;
• упаковка трехмерных контейнеров;
• раскрой фигурных заготовок;
• размещение кругов;
• геометрическое покрытие областей с препятствиями элементами различной формы;
• задача о выборе наилучших размеров материала для последующего раскроя;
• упаковка/покрытие элементами случайных размеров, и многие другие.

Подобные задачи встречаются на практике в машиностроении, металлургии, деревообрабатывающей и швейной промышленности, целлюлозно-бумажной индустрии и др. Многие задачи, на первый взгляд не относящиеся к классу задач раскроя и упаковки, в конечном итоге сводятся к ним. Например, задачи о составлении расписания, задачи маршрутизации, задачи декомпозиции многосвязных ортогональных полигонов, а также многие другие прикладные задачи.

Если ценность раскраиваемого ресурса высока, на практике рассматривают также и остаточные задачи: производится попытка использовать отходы материала, получившиеся при решении предыдущих задач раскроя, упаковки или геометрического покрытия.

Задачи раскроя, упаковки или покрытия могут возникать как промежуточное звено в других задачах или же чередоваться в рамках одной задачи. Например, можно рассмотреть логистическую задачу, где каждому транспортному средству сопоставляется маршрут следования по потребителям и набор соответствующих этим потребителям грузов. Тогда поиск маршрута следования каждого транспортного средства, а также нахождение плана размещения грузов в грузовом отсеке являются задачами класса раскроя-упаковки. Дополнительно при размещении грузов можно учесть порядок следования транспортного средства - так, чтобы грузы, предназначенные последнему клиенту, загружались первыми.

Каждая из предметных областей вносит свои дополнительные требования в способ решения задач, и, следовательно, в способ адаптации известных алгоритмов

3.Метода ньютона-Канторовича приближенного нахождения решений квадратных матричных уравнений 

В настоящее время существующие методы решения нелинейных матричных уравнений очень громоздки и могут быть применены к ограниченным классам уравнений. Поэтому, в настоящей работе была поставлена цель - разработать эффективный приближенный метод решения квадратных матричных уравнений [8].

Рассмотрим квадратное матричное уравнение (1), где все матрицы имеют размерность  [ n × n ]

X² + AX + B = 0                                                (1)

Как известно, метод Ньютона-Канторовича [1, с. 679] решения операторного уравнения F (x) = 0 в банаховом пространстве состоит в построении последовательности 

 

x_n-1 = x _n – [F^ˊ (х_n)] ^-1 F (x_n) (n=1,2,…).        (2)

Для уравнения (1) некоторую трудность представляет нахождение оператора [F^ˊ (х)] ^-1 

Пусть F (X) = X² + AX + B тогда   F(X + H) - F (X) = (X + A) H + HX + H²

 следовательно, дифференциалом левой части уравнения (1) является выражение

F^ˊ  (X) H = (X + A) H + HX                                     (3)

и, таким образом,

[F^ˊ (X)] ^-1 F (X) = H                                              (4)

Равенство (4) означает, что мы должны получить следующее представление для F (X): представить  F (X) в виде равенства X² + AX + B = (X + A)H +HX  и тогда итерационный процесс Ньютона-Канторовича будет иметь следующий вид: 

X_n-1 = X_n - H(X) (n=1,2,...).                                  (5)

Таким образом, возникает следующий алгоритм решения уравнения (1).

1) Найти матричную функцию  H=H (X) - решение линейного по H уравнения

X² + AX + B=(X + A)H + HX                                      (6)

2) Осуществить итерационный процесс (5).

Проиллюстрируем сказанное на примере матриц [2 × 2]

Пусть 

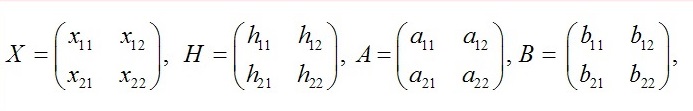
тогда выражение (3) будет иметь вид

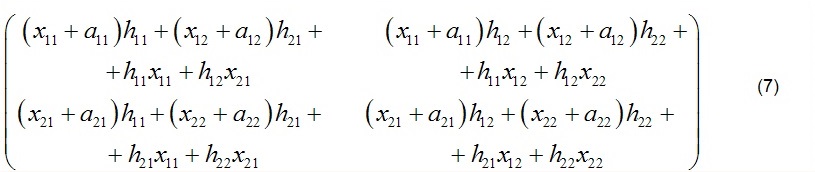
Рассмотрим конкретный пример. Пусть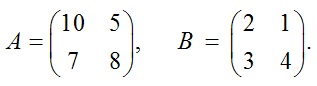  

 

Взяв в качестве начального приближения матрицу 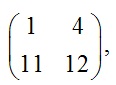 получаем после двадцати итераций корень

 

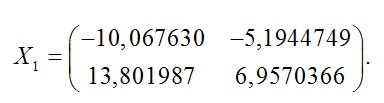
При начальном приближении 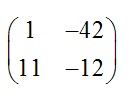 получаем

 

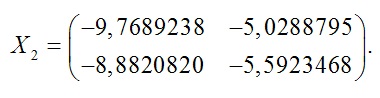
Если начальное приближение    то

 

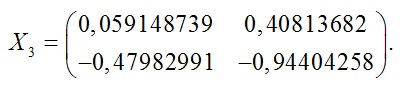
И, наконец, если начальное приближение     то

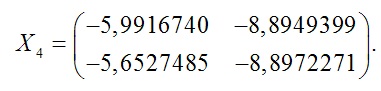
Подставляя найденные значения  в уравнение (1), убеждаемся, что все они являются корнями данного уравнения.

Таким образом, разработан эффективный приближенный метод нахождения решения квадратных матричных уравнений, основанный на использовании модифицированного метода Ньютона-Канторовича.

Многообразие раскройных задач вместе со значимостью их рационального решения обуславливает неугасающий интерес опытных и молодых исследователей всего мира к этой проблематике, с чем связана устойчивая тенденция роста численности новых методик для их решения. В задачах C&P замечательным образом сочетается их широкая практическая применимость и их принадлежность к NP-трудным проблемам, что делает эту проблематику важным полигоном новых исследований. Круг вопросов, решенных или выведенных на новый уровень понимания Канторовичем, столь широк, что невозможно выделить какую-то одну область, работы в которой принесли ему известность. Безусловно, Леонид Витальевич с первых шагов в науке был математиком, а экономикой увлекся значительно позже, когда был уже состоявшимся ученым с мировым именем. Благодаря ему в математике появилась сильнейшая школа функционального анализа и принципиально новое направление - полуупорядоченные пространства. Вклад Канторовича в экономику также сложно переоценить: им была создана абсолютно новая область математических методов - линейное программирование, возникшее на основе его предшествующего математического творчества. Интерес к самых разным вопросам, общим и частным, "постоянное взаимопроникновение теории и практики...", по его собственным словам, - отличительная особенность его характера и склада ума. C другой стороны, такое разнообразие практических приложений методов, разработанных Леонидом Витальевичем, замечательно демонстрирует одну из важнейших установок Петербургской-Ленинградской математической школы, ярким представителем которой был Канторович, - "нет ничего практичнее хорошей теории". Это относится как к использованию Канторовичем в работах по экономики того багажа идей и методов, который уже был накоплен ученым за время математического периода своей научной деятельности, так и к последующему развитию, углублению, обобщению и практическому применению методов ЛП на основе идей, заложенных еще в самой первой работе этого направления.

Список литературы

 

1. Данциг Дж. Б. Линейное программирование, его применение и обобщения. М., 1966. С. 29.
2. Канторович Л. В. Математические методы организации и планирования производства. ЛГУ, 1939. 67 с. . [ L. V. Kantorovich, Mathematical Methods of Production Management and Planning, (in Russian). Leningrad: Leningrad Univ., 1939.]
3. Канторович Л. В. Рациональные методы раскроя металла//Произв.-техн. бюл. НК Боеприпасов СССР. 1942. N 7-8. С. 21-29.
4. Мухачева Э. А., Мухачева А. С., Валеева А. Ф., Картак В. М. Методы локального поиска в задачах ортогонального раскроя и упаковки: аналитический обзор и перспективы развития // Информационные технологии. 2004. N 5. Приложение. С. 2-17. [ E. A. Mukhacheva, et al., "Local search methods in orthogonal cutting-packing problems: analytical survey and development outlook," (in Russian), in Appendix to.
5. Залгаллер В. А. Новое в составлении поставов для распиловки бревен. Л.:ЦНИИЛ "Севзаплес", 1956. Вып. 67.
6. Канторович, Л.В. Функциональный анализ / Л.В. Канторович, Г.П. Акилов. - 3-е изд., перераб. - М.: Наука. Главная редакция физ.-мат. лит-ры, 1984. - 752 с.
7. Flood, M. M. On the Hitchcock Distribution Problem // Pacifi c Journal of Mathematics. 1953. Vol. 3. P. 369-386.